[프로그래머스 / Java] 무인도 여행

문제 링크 : https://school.programmers.co.kr/learn/courses/30/lessons/154540

프로그래머스

 

 

이번 포스팅에서는 프로그래머스의 Level 2 문제인 무인도 여행 문제를 DFS(깊이 우선 탐색) 으로 해결한 방법을 소개하려고 합니다.

BFS보다는 아직 DFS가 더 익숙해서 DFS로 풀었는데요, DFS는 푸는 패턴이 있기 때문에 그 패턴을 익히고 나면 문제에 따라 쉽게 접근할 수 있습니다.

이 포스팅을 통해 문제를 어떻게 접근하고 해결했는지, 그리고 문제를 해결하며 배운 점들을 공유하겠습니다.

 

 

 

 

문제 개요

이 문제의 핵심은 결국 같은 묶음의 원소들을 찾아 누적 합을 구하는 것입니다.

문제에서 예시로 주어진 지도처럼  `{5, 9, 1, 1, 5, 2, 3, 1}`, `{1}`, `{1}` 각각 묶음을 찾아 누적 값을 구해야 합니다.

 

 

접근 방법

저는 이런 식으로 접근하였습니다.

1. 파라미터로 전달받는 `maps`를 2차원 배열인 `graph`로 연결한다. (`X`표시가 아닐 경우에만 `graph`에 넣음.)

2. `graph`의 각 `[i][j]`를 방문한 적이 있는지 확인하기 위해 같은 크기의 `visited`라는 2차원 배열을 만든다.

3. 각 노드에서 `DFS`를 실행하여 현재 인덱스의 상, 하, 좌, 우를 확인하고 연결이 되어 있을 경우에는 `DFS`를 다시 호출하여 `sum`에 값을 더한다.

4. 모든 묶음의 값을 출력

 

알게된 내용

1. 패딩(Padding)

 

graph = new int[M + 2][N + 2];
visited = new boolean[M + 2][N + 2];

 

 

처음 코드를 작성하였을 때는 `maps.length`, `maps[0].length()` 만큼의 길이를 제한하였는데, 인덱스 범위 오류(Index Out of Bounds)가 발생해 이를 방지하고자 +2의 여유를 주었습니다. 이를 패딩 기법이라 하는데요. 패딩을 사용하는 주된 목적은 경계 조건 검사를 단순화 하는 것입니다. 여유 있게 `graph`를 만들어 실제 데이터를 `graph[1][1]`부터 `graph[M][N]`까지 채웁니다.

 

 

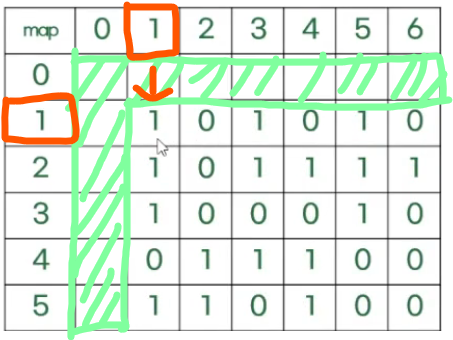
맨 첫 줄에 있는 요소들은 빈 공간으로 채워지는 것이 아니라 int 자료형 초기값인 0으로 자동 초기화 될 것입니다.

 

2. char -> int 파싱은 Character.getNumbericValue()를 사용

 

char c = maps[i].charAt(j);
if (c != 'X') {
    graph[i + 1][j + 1] = Character.getNumericValue(c);
}

 

 

`char`에서 int로 파싱하기 위해서는 `String.valueOf `-> `Integer.parseInt` 총 2번의 파싱의 과정을 거쳐야 한다고 생각했습니다.

찾아보니 `char`에서 `int`로 파싱할 때는 `Character.getNumericValue()`를 사용해 쉽게 파싱할 수 있었습니다.

 

그리고 `maps[i].charAt(j)` 또한 굳이 `String`으로 파싱하여 `equals()`를 사용해 비교하지 않고 `char` 타입이기 때문에 `==` 을 사용해서 비교할 수 있다는 점도 깨달았습니다.

 

 

3. DFS 실행 범위 조정

 

// 3. dfs 실행
for (int i = 1; i <= M; i++) {
    for (int j = 1; j <= N; j++) {
        if (graph[i][j] != 0 && !visited[i][j]) {
            dfs(i, j);
            answer.add(sum);
            sum = 0;
        }
    }
}

 

 

처음 작성한 코드에서는 패딩을 사용하지 않았기 때문에 모든 좌표를 0부터 시작해서 탐색했습니다. 이렇게 할 경우, DFS를 실행하면서 상하좌우를 탐색할 때 항상 경계 바깥으로 넘어가는 상황을 검사해야 합니다. 인덱스 범위 오류(Index Out of Bounds)가 발생할 수 있기 때문입니다.

 

그래서 다음과 같은 조건문을 사용해 경계 검사를 했습니다.

 

if (newY >= 0 && newY < rows && newX >= 0 && newX < cols && graph[newY][newX] != 0 && !visited[newY][newX]) {
    dfs(newY, newX);
}

 

 

이 조건에서 `newY >= 0 && newY < rows && newX >= 0 && newX < cols`는 탐색하려는 좌표가 그래프의 유효한 범위 안에 있는지 검사하는 부분입니다. 이 조건이 없으면 `newY`나 `newX`가 배열의 범위를 벗어나면서 인덱스 범위 오류(Index Out of Bounds)  예외가 발생할 수 있습니다.

 

하지만 패딩을 사용하면 인덱스가 그래프의 유효 범위를 넘어갈 일이 없어집니다. 예를 들어, 탐색 중 `newY`나 `newX`가 `-1`이 되거나 `M` 또는 `N`보다 큰 값이 되더라도, 이 값들은 패딩으로 설정된 `0` 값을 가지는 가장자리에 접근하게 됩니다. 가장자리는 항상 `0`으로 채워져 있기 때문에, `graph[newY][newX] != 0` 조건에서 필터링되기 때문입니다.

 

따라서, 경계를 검사하는 조건식을 추가할 필요가 없어져 아래와 같이 분기문을 간소화할 수 있습니다.

 

if (graph[newY][newX] != 0 && !visited[newY][newX]) {
    dfs(newY, newX);
}

 

 

최종 코드

 

import java.util.ArrayList;
import java.util.Collections;

class Solution {
    static int[][] graph;
    static boolean[][] visited;
    static int sum, M, N;
    static ArrayList<Integer> answer = new ArrayList<>();

    static int dirX[] = { 0, 0, -1, 1 };
    static int dirY[] = { -1, 1, 0, 0 };

    static void dfs(int y, int x) {
        visited[y][x] = true;
        sum += graph[y][x];
        for (int i = 0; i < 4; i++) {
            int newY = y + dirY[i];
            int newX = x + dirX[i];
            if (graph[newY][newX] != 0 && !visited[newY][newX]) {
                dfs(newY, newX);
            }
        }
    }

    public ArrayList<Integer> solution(String[] maps) {
        M = maps.length;
        N = maps[0].length();

        graph = new int[M + 2][N + 2];
        visited = new boolean[M + 2][N + 2];

        // 1. graph 연결
        for (int i = 0; i < M; i++) {
            for (int j = 0; j < N; j++) {
                char c = maps[i].charAt(j);
                if (c != 'X') {
                    graph[i + 1][j + 1] = Character.getNumericValue(c);
                }
            }
        }

        // 2. dfs 실행
        for (int i = 1; i <= M; i++) {
            for (int j = 1; j <= N; j++) {
                if (graph[i][j] != 0 && !visited[i][j]) {
                    dfs(i, j);
                    answer.add(sum);
                    sum = 0;
                }
            }
        }

        // 3. 출력
        if (answer.isEmpty()) {
            answer.add(-1);
        } else {
            Collections.sort(answer);
        }

        return answer;
    }
}

 

 

마치며

이번 문제를 통해 DFS에 대해 다시 한 번 익힐 수 있었습니다.

DFS 문제의 경우 패턴이 정해져 있기 때문에 DFS보다 SUM을 어느 위치에 두어야 하는지를 파악해야 하는 문제였다고 생각합니다. 이후에는 그림을 그려 왜 해당 위치에 SUM을 두어야 하는지 이해하는 시간도 필요하다 생각하였습니다.