[백준 / Java] 1987번 알파벳

문제 링크 : https://www.acmicpc.net/problem/1987

1987번: 알파벳

 

 

이번 포스팅에서는 백준 골드 4문제인 알파벳 문제를 DFS(깊이 우선 탐색)으로 해결한 방법을 작성하고자 합니다.

백트래킹 문제를 처음 접해 백트래킹이 무엇인지조차 잘 모르는 상태에서 문제를 풀어보았는데요.

이 포스팅을 통해 백트래킹이 무엇인지, 문제를 어떻게 접근하고 해결했는지, 그리고 문제를 해결하며 배운 점들을 공유하겠습니다.

 

백트래킹(backtracking)이란?

백트래킹은 가능한 모든 경우의 수를 탐색하는 과정에서, 해답이 될 가능성이 없는 경우를 조기에 포기하는 방식으로, 불필요한 탐색을 줄이는 것이 핵심입니다.

쉽게 말해, 백트래킹은 `DFS`를 기반으로 한 기법이지만, 탐색 중 가지치기(pruning)를 통해 경로를 줄여 효율성을 높이는 문제입니다.

 

 

 

 

문제 개요

이 문제는 다른 `DFS` 유형과 비슷하지만 방문한 적이 없는 알파벳의 경로로만 갈 수 있는 조건이 추가된 백트래킹 문제입니다.

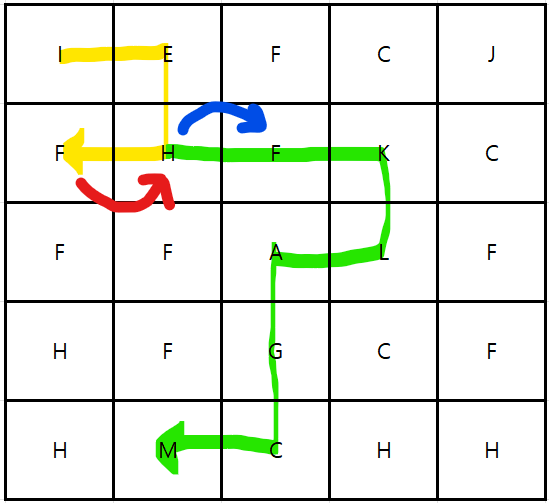
예시 이미지를 기준으로 `I -> E -> H -> F`로 갔을 때 `F` 기준으로 방문하지 않은 노드는 아래에 있는 `F`만 해당이 됩니다.

이때 `F`라는 알파벳은 이미 `Set`에 담겨 있기 때문에 다시 `H`로 돌아와서 `H`의 왼쪽이 아닌 오른쪽으로 탐색을 해야 합니다.

결국 최장 경로는 `I -> E -> H -> F -> K -> L -> A -> G -> C -> M` 루트로 `depth`는 10이 출력이 되게 됩니다.

 

일반 `DFS` 문제와 크게 다르진 않지만 이전에 방문한 적이 있는 알파벳 노드로 이동하지 않는 조건으로 최장 경로를 구하는 것이 핵심입니다.

이를 위해 `HashSet`과 `depth` 변수를 추가하여 탐색을 진행합니다.

 

 

접근 방법

저는 이런 식으로 접근하였습니다.

1. `graph` 정보를 char 타입이 아닌 int 타입으로 변환하여 사용했습니다. 이로 인해 간단한 숫자 비교로 탐색을 진행할 수 있었습니다.

2. `graph`의 각 `[i][j]`를 방문한 적이 있는지 확인하기 위해 같은 크기의 `visited`라는 2차원 배열을 만들었습니다.

3. 시작점(1행 1열)부터 `DFS`를 실행하고, 현재 위치에 있는 알파벳을 `HashSet`에 추가하여 방문을 기록했습니다.

이후 아직 방문한 적이 없고, `HashSet`에 포함되지 않은 알파벳인 경우에만 `DFS`를 재귀적으로 호출하며 `depth`를 증가시켰습니다.

4. 이때 최장 경로를 찾기 위해 모든 경로를 탐색하되, 탐색이 종료된 이후에는 `HashSe`t과 `visited` 배열에서 해당 알파벳 및 위치 정보를 제거하여 백트래킹을 수행했습니다.

5. 탐색이 완료된 후, 최종적으로 `depth`에 가장 긴 경로의 길이가 담겨있기 때문에 `depth`를 출력합니다.

 

알게 된 내용

1. depth

변경 전

if (visited[ny][nx] && !set.contains(graph[ny][nx])) {
    answer++;
    dfs(ny, nx);
}

 

변경 후

maxPath = Math.max(maxPath, depth);

 

 

처음에는 `answer`라는 변수를 사용하여 `DFS`가 호출될 때마다 `depth`를 증가시키는 방식으로 구현했습니다.

하지만 이 경우 백트래킹 시 깊이를 조정하는 것이 어려워져서 `depth`를 함수 매개변수로 넘기며 관리하는 방식으로 변경했습니다.

탐색 중 각 깊이를 쉽게 추적하고, 최장 경로를 구해야 할 때는 `answer`를 쓰는 것이 아니라 `depth`를 써야 한다는 것을 알게 되었습니다.

 

 

2. HashSet

문제를 읽고 처음에는 `Queue`를 사용하려고 했습니다. `Queue`에도 `contains()` 메서드가 있어서 알파벳을 비교하는 데 사용할 수 있다고 생각했기 때문입니다. 그러나 이 문제에서는 알파벳의 존재 여부만 빠르게 확인하면 되므로, `HashSet`이 가장 적합한 자료구조라는 것을 알게 되었습니다.

`HashSet`은 중복을 허용하지 않고 탐색 시 `O(1)`로 효율적으로 접근할 수 있다는 장점이 있습니다.

 

 

 

3. 백트래킹 과정에서의 처리

이 부분이 가장 어렵고 해결에 시간이 많이 걸렸는데요.

 

visited[y][x] = false;
set.add(graph[y][x]);
for (int i = 0; i < 4; i++) {
    int ny = y + dirY[i];
    int nx = x + dirX[i];

    if (visited[ny][nx] && !set.contains(graph[ny][nx])) {
        dfs(ny, nx, depth + 1);
    }
}
set.remove(graph[y][x]);
visited[y][x] = true;

 

 

탐색이 끝나고 이전 단계로 되돌아갈 때(백트래킹)는 반드시 현재 위치의 방문 기록을 초기화해야 합니다.

방문 기록을 초기화하지 않을 경우에는 `set`과 `visited`에 방문 기록이 남아 있기 때문에 원하는 결과를 얻을 수 없습니다.

따라서 백트래킹 과정에서 `set.remove()`와 `visited[y][x] = true`를 통해 모든 탐색이 끝난 후 상태를 되돌려 주는 것이 중요합니다.

저는 `visited`를 `graph`에 정보를 넣을 때 `true`로 초기화 한 후 `DFS` 과정을 거치면서 `false`로 변환하게끔 코드를 구현했기 때문에 여기서는 `visited[y][x] = false` 대신 `true`로 선언했습니다.

 

 

최종 코드

 

import java.io.*;
import java.util.*;

class Main {
    static int[][] graph;
    static boolean[][] visited;
    static int N, M;
    static HashSet<Integer> set = new HashSet<>();
    static int maxPath = 0;

    static int[] dirY = {-1, 1, 0, 0};
    static int[] dirX = {0, 0, -1, 1};

    static int dfs(int y, int x, int depth) {
        maxPath = Math.max(maxPath, depth);

        visited[y][x] = false;
        set.add(graph[y][x]);
        for (int i = 0; i < 4; i++) {
            int ny = y + dirY[i];
            int nx = x + dirX[i];

            if (visited[ny][nx] && !set.contains(graph[ny][nx])) {
                dfs(ny, nx, depth + 1);
            }
        }
        set.remove(graph[y][x]);
        visited[y][x] = true;
        return maxPath;
    }

    public static void main(String[] args) throws IOException {

        // 0. 입력 및 초기화
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());
        M = Integer.parseInt(st.nextToken()); // y
        N = Integer.parseInt(st.nextToken()); // x

        graph = new int[M + 2][N + 2];
        visited = new boolean[M + 2][N + 2];

        // 1. graph 정보 반영
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            StringBuilder str = new StringBuilder(st.nextToken());

            for (int j = 0; j < N; j++) {
                char c = str.charAt(j);
                graph[i + 1][j + 1] = Character.getNumericValue(c);
                visited[i + 1][j + 1] = true;
            }
        }

        // 2. dfs 수행
        dfs(1, 1, 1);

        // 3. 출력
        bw.write(String.valueOf(maxPath));
        bw.newLine();

        bw.close();
        br.close();
    }
}

 

 

마치며

이번 문제는 백트래킹에 대해 잘 알고 있다면 쉽게 풀 수 있는 문제였지만, 처음 백트래킹을 접했기 때문에 2시간 30분이라는 긴 시간이 소요되었습니다. 글로 다시 풀이를 정리함으로써 백트래킹의 개념과 가지치기의 중요성을 깨달을 수 있었고, 문제 해결을 위해 여러 번의 시행착오를 겪으면서 백트래킹 문제에 흥미를 느끼게 되었습니다.

 

특히, 탐색을 진행하며 방문했던 알파벳의 경로를 어떻게 관리할지와, 백트래킹을 통해 탐색이 끝난 후 상태를 원래대로 되돌리는 과정의 중요성을 깊이 깨달았습니다.  이 과정에서 `set.remove()`의 정확한 위치와 `visited` 배열의 원복을 놓치지 않는 것이 문제 해결에 중요한 요소임을 이해하게 되었고, 이로 인해 백트래킹의 핵심 로직을 명확히 잡을 수 있었습니다.

 

이 문제를 해결하며 백트래킹을 포함한 탐색 기법의 매력을 느끼게 되었고, 코딩 스터디에서 진행하는 페어프로그래밍이 큰 도움이 되어 앞으로 더 어려운 문제도 접근할 수 있을 것 같은 자신감이 생겼습니다.